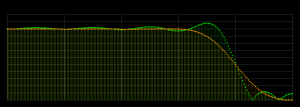
FIRフィルタのゲイン特性を描画する
思い出すのに苦労したけど、FIRの係数を算出できたので、
せっかくだからゲイン特性の描画もやってみた。
use v5.14;
use strict;
use warnings;
use Imager;
use Math::Trig qw/pi/;
use List::Util qw/sum/;
use constant STEP_X => 4;
use constant SCALE_Y => 200.0;
use constant FIR_TAP => 19;
use constant SPECTRUM_SIZE => 201;
# グラフの描画に必要な最低限の幅(先端のマークを含まず)
my $graph_width = 1 + (STEP_X * (SPECTRUM_SIZE - 1));
my $graph_height = SCALE_Y + 1;
my ( $width, $height ) = ( $graph_width + 40, $graph_height + 100 );
my ( $x0, $y0 ) = ( int(($width - $graph_width) / 2), ($height - 20) );
say '=-' x 10, ' ', FIR_TAP, ' ', '=-' x 10;
if (1) {
my $fir_tap = FIR_TAP;
my $img = Imager->new(
xsize => $width, ysize => $height, channels => 4 );
draw_graduation( $img, Imager::Color->new(64,64,64) );
my $fc = 0.4;
my $fir = fir_lpf( $fir_tap, $fc );
my $window = hamming_window( $fir_tap );
my $fir2 = apply_window( $fir, $window );
$fir = normalize( $fir );
$fir2 = normalize( $fir2 );
my $n = SPECTRUM_SIZE - 1;
my @data1 = map { calc_gain( $fir, $_ / ($n * 2) ); } 0..$n;
draw_spectrum( $img, \@data1, 'green' );
my @data2 = map { calc_gain( $fir2, $_ / ($n * 2) ); } 0..$n;
draw_spectrum( $img, \@data2, 'orange' );
my $dst_file = sprintf( 'fir_gain_%02d.png', $fir_tap );
$img->write( file => $dst_file ) or die $img->errstr;
}
sub normalize {
my $fir = shift;
my $gain = 1.0 / sum( @{$fir} );
my @ret = map {
$_ * $gain;
} @{$fir};
return \@ret;
}
sub apply_window {
my ( $fir, $window ) = @_;
my $n = @{$fir};
my @ret = map {
$fir->[$_] * $window->[$_];
} 0..($n - 1);
return \@ret;
}
sub fir_lpf {
my ( $n, $fc ) = @_;
my @fir = map {
my $i = $_ - int($n / 2);
if ( $i ) {
sin(2.0 * $i * pi() * $fc) / ($i * pi());
}
else {
2.0 * $fc;
}
} 0..($n - 1);
return \@fir;
}
sub kaiser_window {
my ( $n, $alpha ) = @_;
my @ret = map {
bessel( $alpha * sqrt(1.0 - ($_ ** 2.0)) ) / bessel( $alpha );
} map {
($_ - int($n / 2)) / int($n / 2);
} 0..($n - 1);
#printf( "%2d: %.3f\n", $_, $ret[$_] ) for 0..($n - 1);
return \@ret;
}
sub hann_window {
my $n = shift;
my @ret = map {
my $x = 2.0 * pi() * $_;
0.5 + (0.5 * cos($x));
} map {
($_ - int($n / 2)) / ($n - 1);
} 0..($n - 1);
return \@ret;
}
sub hamming_window {
my $n = shift;
my @ret = map {
my $x = 2.0 * pi() * $_;
0.54 + (0.46 * cos($x));
} map {
($_ - int($n / 2)) / ($n - 1);
} 0..($n - 1);
return \@ret;
}
sub bessel {
my $x = shift;
my $total = 1;
my $factorial = 1;
foreach my $n ( 1..20 ) {
$factorial *= $n;
my $tmp = (($x / 2) ** $n) / $factorial;
$total += ($tmp * $tmp);
}
#say $total;
return $total;
}
sub calc_gain {
my ( $params, $w ) = @_;
# H(z) = h0 + h1 * z^-1 + h2 * z^-2 + ...
# z^1 = e^(jw) = cos(w) + j*sin(w)
# z^-1 = e^(-jw) = cos(w) - j*sin(w)
# H(jw) = A - jB
# |H(jw)| = sqrt( A^2 + B^2 )
my @h = @{$params};
my $n = scalar( @{$params} );
my $re = sum( map {
$h[$_] * cos( 2.0 * pi * $_ * $w );
} 0..($n - 1) );
my $im = sum( map {
-1.0 * $h[$_] * sin( 2.0 * pi * $_ * $w );
} 0..($n - 1) );
return sqrt( ($re * $re) + ($im * $im) );
}
sub draw_spectrum {
my ( $img, $data, $color ) = @_;
my $img_tmp = Imager->new(
xsize => $img->getwidth(), ysize => $img->getheight(), channels => 4 );
my $n = scalar( @{$data} );
for (my $i=0; $i<$n; $i++) {
my $dx = $i * STEP_X;
my $dy = int($data->[$i] * SCALE_Y);
$img_tmp->line(
x1 => ($x0 + $dx), y1 => $y0,
x2 => ($x0 + $dx), y2 => ($y0 - $dy),
color => $color );
}
$img->compose( src => $img_tmp, opacity => 0.25, combine => 'add' );
for (my $i=0; $i<$n; $i++) {
my $dx = $i * STEP_X;
my $dy = int($data->[$i] * SCALE_Y);
my ( $x, $y ) = ( ($x0 + $dx), ($y0 - $dy) );
$img->box(
xmin => $x - 1, ymin => $y - 1, xmax => $x + 1, ymax => $y + 1,
color => $color, filled => 0 );
}
}
sub draw_graduation {
my ( $img, $color ) = @_;
$img->box( filled => 1, color => 'black' );
for ( 0..6 ) {
my $x = $x0 + ((($graph_width - 1) / 5) * $_);
$img->line(
x1 => $x, y1 => $y0,
x2 => $x, y2 => $y0 - (($graph_height - 1) * 1.2),
color => $color );
}
for ( 0..12 ) {
my $y = $y0 - ((SCALE_Y / 10) * $_);
$img->line(
x1 => $x0, y1 => $y,
x2 => $x0 + ($graph_width - 1), y2 => $y,
color => $color );
}
}
ちょいちょい余計なコードが残ってるけどご愛嬌ということで。
IIRのゲイン特性の計算(*1)を見ながらやったので、
思ったより簡単にできた。
おしまい。
(*1) https://github.com/techno-cat/p5-Cassis/blob/master/Samples/amplitude_spectrum.pl
Leave a Comment