帰ってきたネコブログ

コッホ曲線を描くスクリプトをいじってたら出来ちゃいました。

use v5.14;
use strict;
use warnings;

use Imager;

use constant N => 9;
use constant WIDTH => 600;
use constant HEIGHT => 600;

my $margin = 50;
my ( $x0, $y0 ) = ( 0, HEIGHT - $margin );

my @gen = (
    [ 0.6,  0.3 ],
    [ 0.6, -0.3 ]
);

my $lines = [
    [
        [ 300,  0 ],
        [ 300,  150 ]
    ]
];

my $img = Imager->new(
    xsize => WIDTH, ysize => HEIGHT );

foreach my $n ( 0..N ) {
    $img->box( filled => 1, color => 'white' );

    if ( 0 < $n ) {
        say "lines = ", scalar(@{$lines}), ", \$n = ", scalar(@gen) ** ($n - 1);
        $lines = generate( $lines, scalar(@gen) ** ($n - 1) );
    }

    foreach my $line ( @{$lines} ) {
        my @tmp = map {
            [ int($x0 + $_->[0]), int($y0 - $_->[1]) ];
        } @{$line};
        $img->polyline( points => \@tmp, color => 'black' );
    }

    my $dst_file = ($0 =~ s/\.pl//r) . "_${n}.png";
    $img->write( file => $dst_file ) or die $img->errstr;
}

sub generate {
    my $lines = shift;
    my $n = shift;

    my @result = @{$lines};
    for (my $i=1; $i<=$n; $i++) {
        my $line = $lines->[-$i];
        my ( $st, $en ) = @{$line};

        my $dx = $en->[0] - $st->[0];
        my $dy = $en->[1] - $st->[1];

        push @result, map {
            my ( $x, $y ) = ( $_->[0], $_->[1] );
            # x2 = $x * cos(a) - $y * sin(a) + st.x;
            # y2 = $x * sin(a) - $y * cos(a) + st.y;
            # sin(a) = dy / 1.0, cos(a) = dx / 1.0
            [
                $en,
                [
                    ($x * $dx) - ($y * $dy) + $en->[0],
                    ($x * $dy) + ($y * $dx) + $en->[1]
                ]
            ];
        } @gen;
    }

    return \@result;
}

追加した枝の数を渡して、そこから枝を作って・・・、
みたいな感じの実装になっております。
どんどん線分が増えてアレな感じもしますが、
最終的にSVGを出力するなら、これで良いような気がします。
どうしても気になるようなら、参照しない枝は先に出力してしまうとか、
方法はいろいろあるんじゃないですかね。

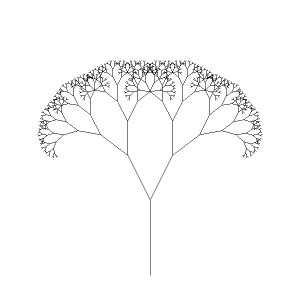
という訳で、このスクリプトの実行結果はこんな感じ。

おしまい。

カテゴリー: Perl, コンピューター by ネコ on 2015年05月13日 | タグ: Imager > フラクタル > メモ