帰ってきたネコブログ

正規乱数の勉強をしようと思ったんだけど、
Math::Random::NormalDistributionのコードを見てたら、
ボックスミュラー法なるものを実装してて、
コードがすごいあっさりしてて良く分からなかったので、
以前うまくいかなかった透過周りをリベンジすることにした。

use v5.14;
use strict;
use warnings;

use Imager;
use Math::Random::NormalDistribution;

use constant N => 200000;
use constant STEP_X => 3;

my ( $width, $height ) = ( 401, 311 );
my ( $x0, $y0 ) = ( int($width / 2), ($height - 11) );

my $img = Imager->new(
    xsize => $width, ysize => $height, channels => 4 );

draw_graduation( $img, Imager::Color->new(64,64,64) );

draw_noise( $img, 0.0, 0.1, 'orange' );
draw_noise( $img, 0.0, 0.2, 'green' );

$img->write( file => 'rand.png' ) or die $img->errstr;

sub draw_noise {
    my ( $img, $mean, $stddev, $color ) = @_;

    my $gen = rand_nd_generator( $mean, $stddev );

    my %hist = ();
    foreach ( 1..N ) {
        my $tmp = $gen->() * 50;
        $tmp = ( $tmp < .0 ) ? int($tmp - 0.5) : int($tmp + 0.5);
        if ( exists $hist{$tmp} ) {
            $hist{$tmp}++;
        }
        else {
            $hist{$tmp} = 1;
        }
    }

    my $img_tmp = Imager->new(
        xsize => $img->getwidth(), ysize => $img->getheight(), channels => 4 );

    foreach my $dx ( keys %hist ) {
        my $dy = int($hist{$dx} / 100);

        if ( 0 < $dy ) {
            $img_tmp->line(
                x1 => ($x0 + ($dx * STEP_X)), y1 => $y0,
                x2 => ($x0 + ($dx * STEP_X)), y2 => ($y0 - $dy),
                color => $color );
        }
    }

    $img->compose( src => $img_tmp, opacity => 0.25, combine => 'add' );

    foreach my $dx ( keys %hist ) {
        my $dy = int($hist{$dx} / 100);

        my ( $x, $y ) = ( $x0 + ($dx * STEP_X), $y0 - $dy );
        $img->box(
            xmin => $x - 1, ymin => $y - 1, xmax => $x + 1, ymax => $y + 1,
            color => $color, filled => 0 );
    }
}

sub draw_graduation {
    my ( $img, $color ) = @_;

    $img->box( filled => 1, color => 'black' );

    $img->line(
        x1 => $x0, y1 => $y0,
        x2 => $x0, y2 => 0,
        color => $color );
    $img->line(
        x1 => 0, y1 => $y0,
        x2 => ($width - 2), y2 => $y0,
        color => $color );
}

とにかくきれいな正規分布が描けるように、
サンプル数を増やしつつ、グラフをはみ出さないように割り算して、
目盛とか意味をなさない感じになったので、軸だけ残した。

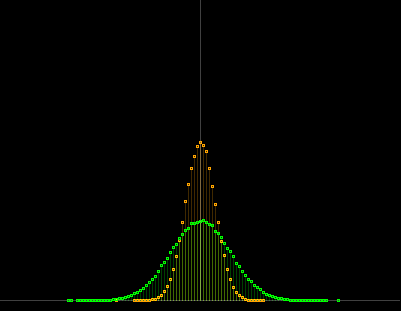
で、これを実行するとこんな感じ。

結局、透過の方法が分からなかったので、
同じサイズのバッファを用意して、うまいこと重ねることにした。
詳しくは、Imager::Transformationsにある、composeを見て頂ければと思う。

おしまい。

カテゴリー: Perl, コンピューター by ネコ on 2014年11月04日 | タグ: Imager > アルゴリズム > メモ